Costruzione di un Poligono di “N” lati

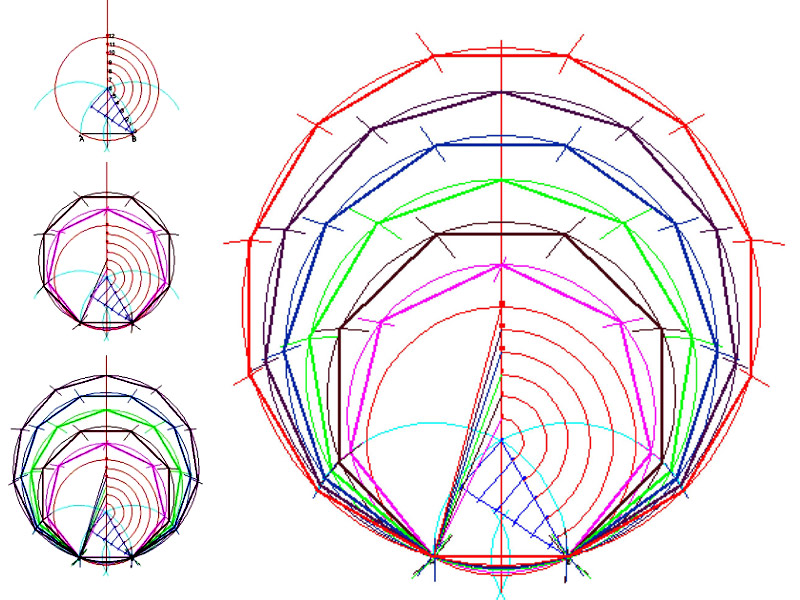
Costruzione geometrica con riga e compasso

Partendo dal lato AB si costruisce l’asse del segmento e con raggio AB, puntando prima in A e poi in B si tracciano due archi che s’incontrano nel punto 6.

Si divide 6B in sei parti uguali, che si chiamano 0, quello coincidente con B, e, successivamente, 1,2,3,4,5, fino al 6 già trovato in precedenza (in blu: costruzione di “Talete”).

Si ribaltano i punti ottenuti sull’asse del segmento e si attribuiscono, per comodità, i numeri 7, 8, 9, 10, 11, 12, alle intersezioni con detto asse.

Eptagono (7 lati)

Puntando in 7, con raggio 7 si costruisce una circonferenza.

Sulla circonferenza, partendo da A e da B, si riportano degli archi di circonferenza di raggio AB, fino ad ottenere un eptagono.

Ottagono (8 lati)

Puntando in 8, con raggio 8-A si costruisce una circonferenza.

Sulla circonferenza, partendo da A e da B, si riportano degli archi di circonferenza di raggio AB, fino ad ottenere un ottagono.

Ennagono (9 lati)

Puntando in 9, con raggio 9-A si costruisce una circonferenza.

Sulla circonferenza, partendo da A e da B, si riportano degli archi di circonferenza di raggio AB, fino ad ottenere un ennagono.

Decagono (10 lati)

Puntando in 10, con raggio 10-A si costruisce una circonferenza.

Sulla circonferenza, partendo da A e da B, si riportano degli archi di circonferenza di raggio AB, fino ad ottenere un decagono.

Endecagono (11 lati)

Puntando in 11, con raggio 11-A si costruisce una circonferenza.

Sulla circonferenza, partendo da A e da B, si riportano degli archi di circonferenza di raggio AB, fino ad ottenere un endecagono.

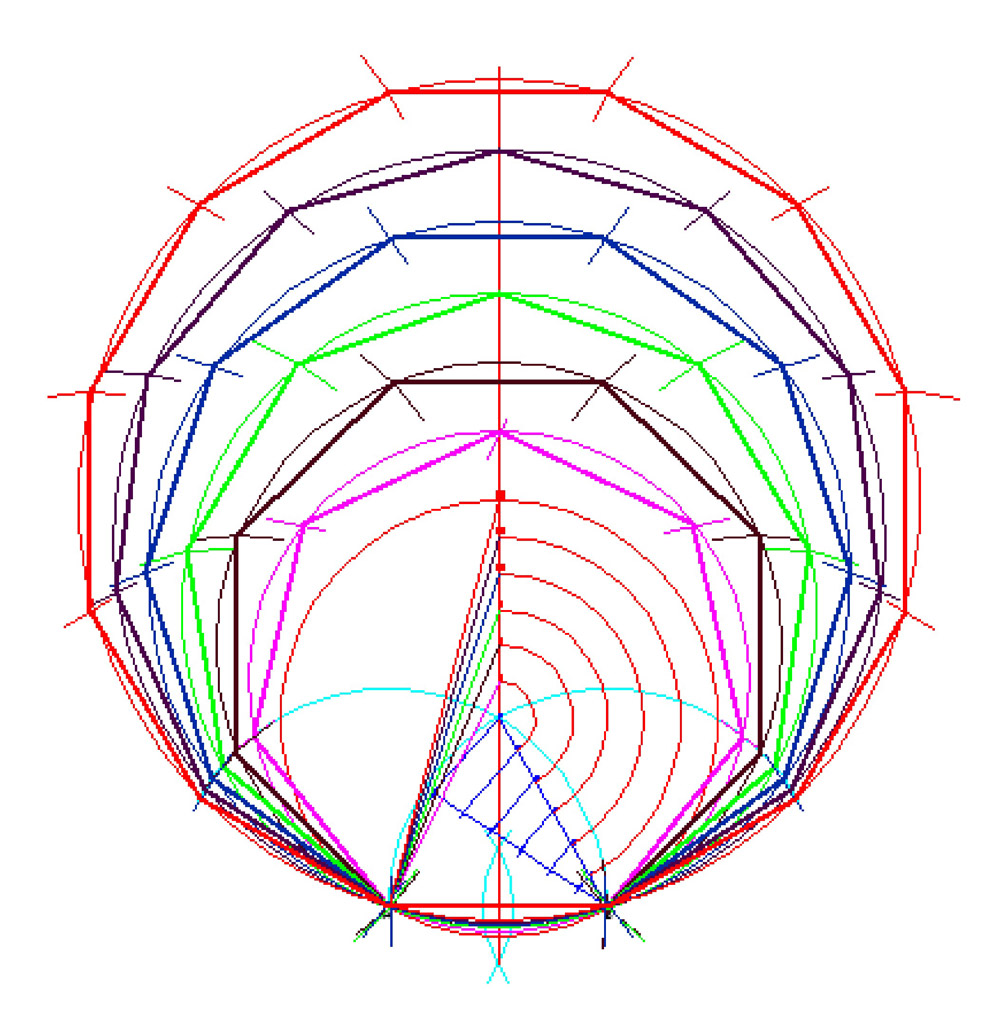Dodecagono (12 lati)

Puntando in 12, con raggio 12-A si costruisce una circonferenza.

Sulla circonferenza, partendo da A e da B, si riportano degli archi di circonferenza di raggio AB, fino ad ottenere un dodecagono.