The Fibonacci sequence
A method for deriving a numerical sequence
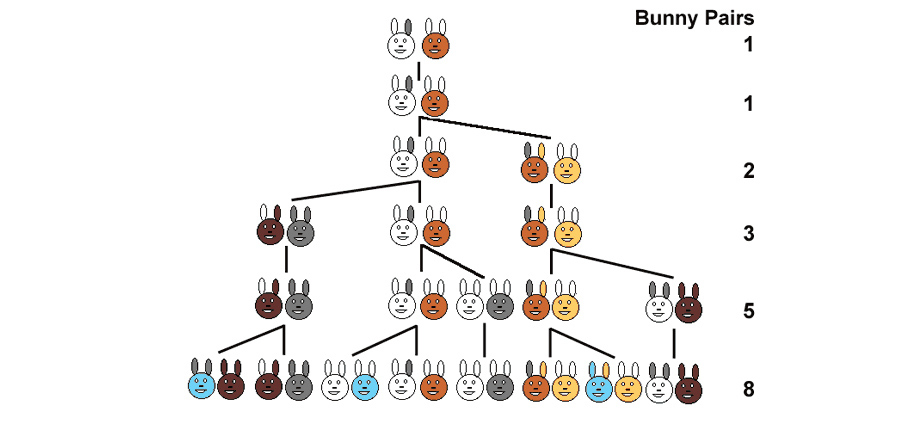
The problem from which Fibonacci started (year 1202) as a family of rabbits could be developed in ideal circumstances.

Suppose we have a pair of rabbits (male and female).
Rabbits are able to reproduce at the age of one month so by the end of her second month a female can produce another pair of rabbits.
Suppose that our rabbits never die and that the female always produces a new pair (a male and a female) every month from the second month onwards.
The problem posed by Fibonacci was: how many pairs will there be after one year?
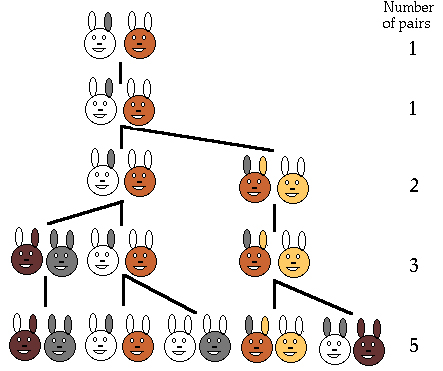
The number of rabbit pairs at the beginning of each month will be 1, 1, 2, 3, 5, 8, 13, 21, 34, …
It is clear that each term in the series can be obtained by adding the two immediately preceding terms, so the next term in the series indicated above will be given by 21 + 34 = 55.
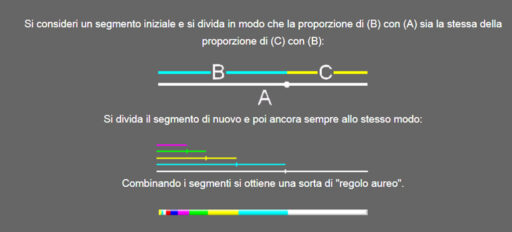
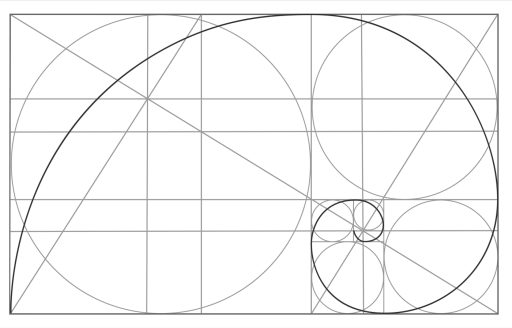
It is possible to verify that by proceeding with the development of the series a numerical succession is obtained which increasingly approximates a geometric progression of reason Ø fi (golden section ratio corresponding to approximately 1.618)
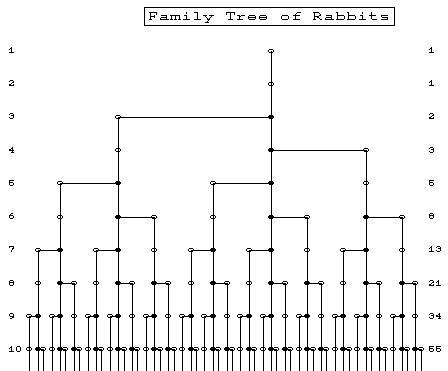
The tree above shows how this result is achieved.
All this might seem like a pure mathematical curiosity linked to the particularity of this problem and to purely random factors. Of considerable interest, however, is the recurring presence of these numbers in multiple natural situations (animals and plants) such as to induce numerous artists to recognize in this numerical sequence a sort of natural order which accords well with the harmony induced by the golden ratio ratio. .
The whole part about the Fibonacci problem and the related images were prepared by: © Dr Ron Knott R.Knott@surrey.ac.uk . The Italian version was edited by Franco Di Cataldo for exclusive educational use.