La successione di Fibonacci
Un metodo per ricavare una successione numerica
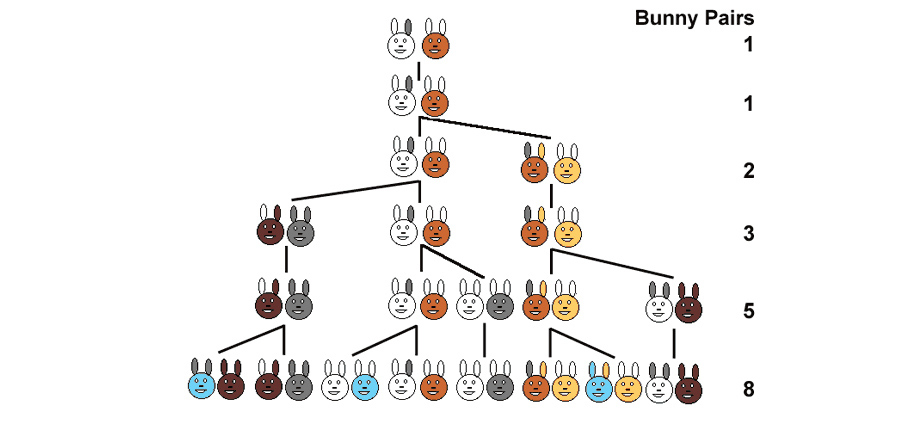
Il problema da cui partì Fibonacci (anno 1202) come una famiglia di conigli si poteva sviluppare in circostanze ideali.

Supponiamo di avere una coppia di conigli (maschio e femmina).
I conigli sono in grado di riprodursi all’età di un mese per cui alla fine del suo secondo mese una femmina può produrre un’altra coppia di conigli.
Supponiamo che i nostri conigli non muoiano mai e che la femmina produca sempre una nuova coppia (un maschio ed una femmina) ogni mese dal secondo mese in poi.
Il problema posto da Fibonacci fu: quante coppie ci saranno dopo un anno?
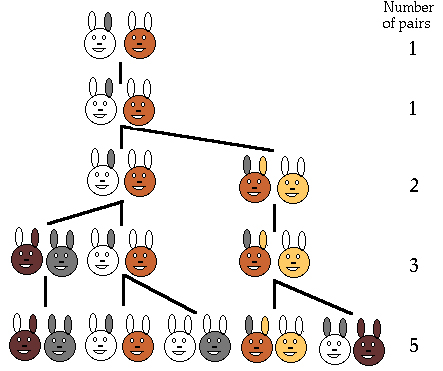
Il numero delle coppie di conigli all’inizio di ciascun mese sarà 1, 1, 2, 3, 5, 8, 13, 21, 34, …
E’ evidente che ciascun termine della serie si può ottenere sommando i due termini immediatamente precedenti, per cui il termine successivo nella serie indicata sopra sarà dato da 21 + 34 = 55.
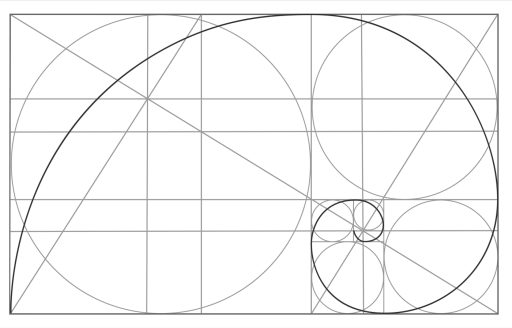
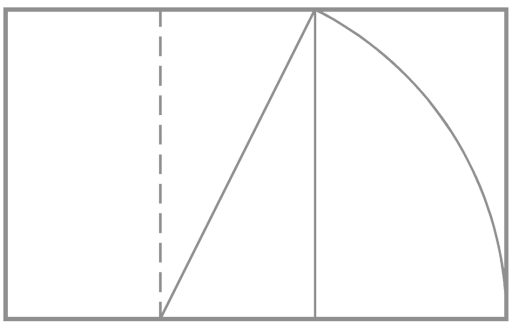
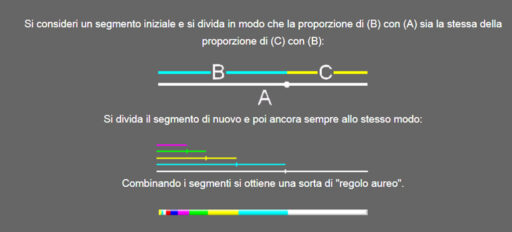
E’ possibile verificare che procedendo nello sviluppo della serie si ottiene una successione numerica che approssima sempre di più una progressione geometrica di ragione Ø fi (rapporto di sezione aurea corrispondente a circa 1,618)
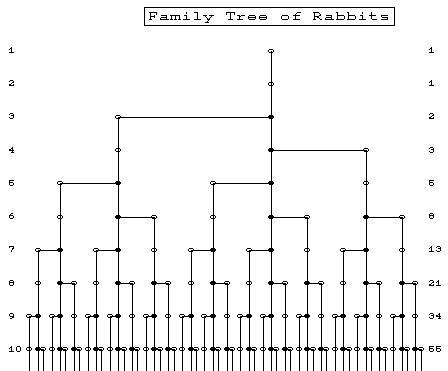
Nell’albero riportato di sopra si mostra come si perviene a questo risultato.
Tutto questo potrebbe sembrare una pura curiosità matematica legata alla particolarità di questo problema ed a fattori puramente casuali. Di notevole interesse risulta tuttavia la ricorrente presenza di questi numeri in molteplici situazioni naturali (animali e piante) tali da indurre numerosi artisti a riconoscere in questa sequenza numerica una sorta di ordine naturale che ben si accorda con l’armonia indotta dal rapporto di sezione aurea.
Tutta la parte sul problema di Fibonacci e le relative immagini sono state elaborate da: © Dr Ron Knott R.Knott@surrey.ac.uk . La versione italiana è stata curata da Franco Di Cataldo per esclusivo uso didattico.