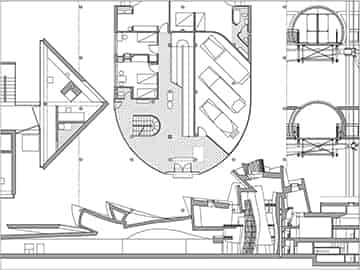
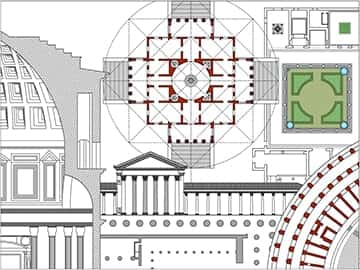
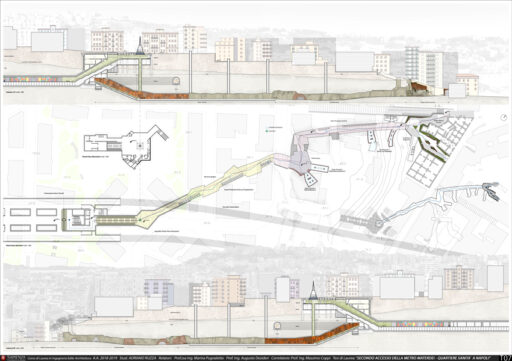
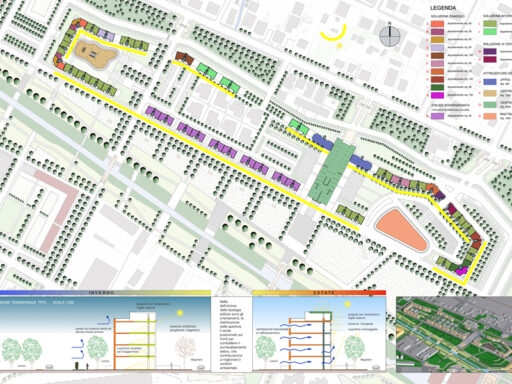
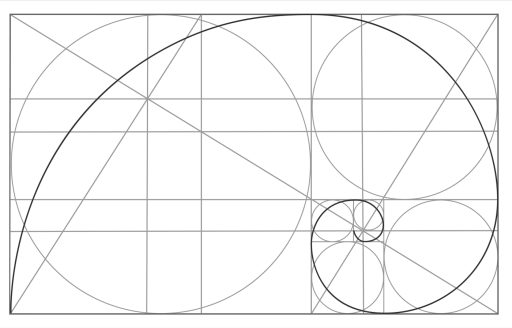
Rettangolo Aureo

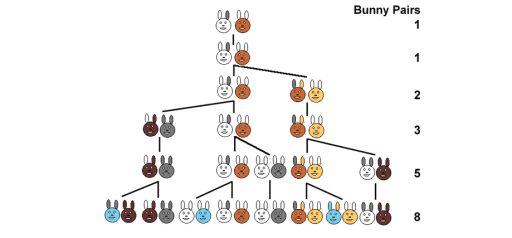
SEZIONE  AUREA, CRESCITA  E  SERIE  DI  FIBONACCI

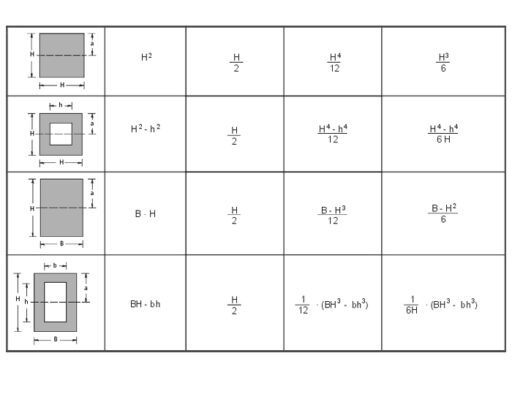
Il rettangolo aureo, anche noto come rettangolo d’oro o rapporto aureo, è un rapporto particolare tra le lunghezze dei lati di un rettangolo. Si dice che un rettangolo sia aureo se il rapporto tra la lunghezza del lato più lungo e quella del lato più corto è approssimativamente uguale al rapporto tra la somma delle due lunghezze e la lunghezza del lato più lungo. Matematicamente, questo rapporto è approssimativamente uguale a 1,6180339887… e viene spesso rappresentato con la lettera greca φ (phi). Questo rapporto è stato ritenuto esteticamente gradevole ed è stato utilizzato in molte opere d’arte e architettoniche.

Ø (fi), fu descritto da Johannes Keplero come uno dei “due grandi tesori della geometria” (l’altro era il teorema di Pitagora).
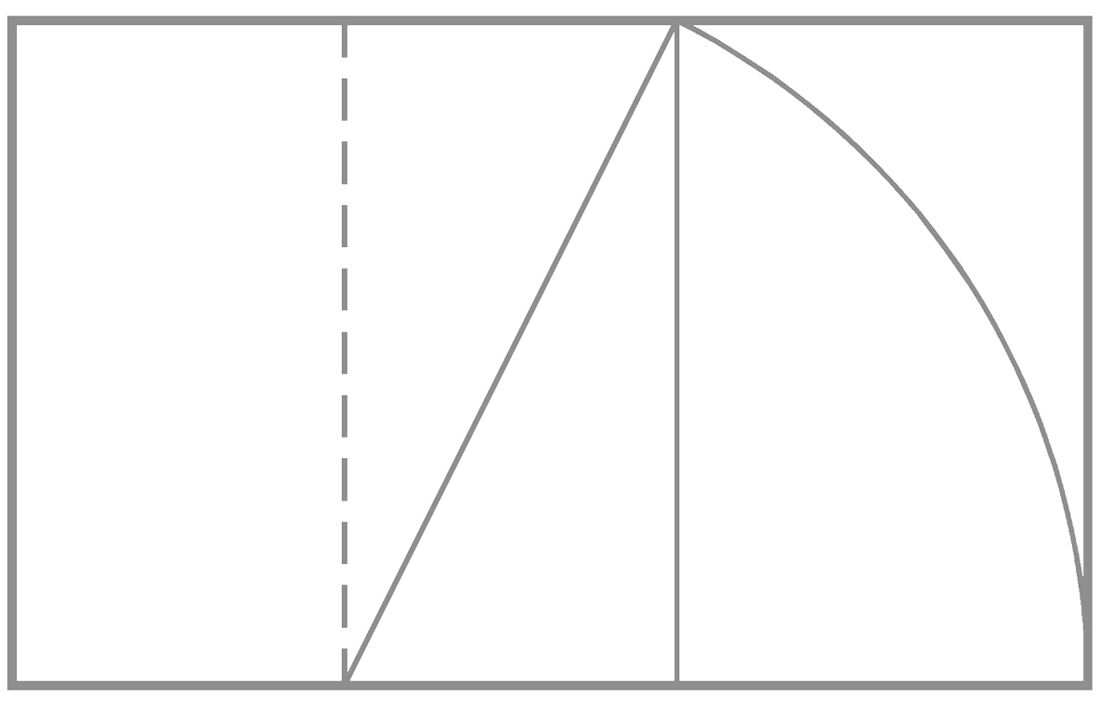
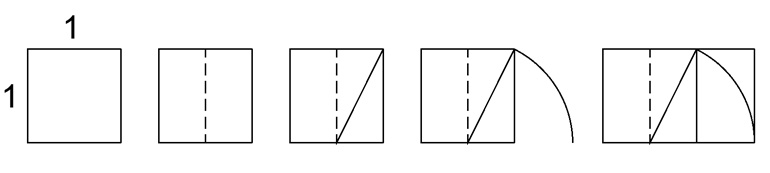
Il rettangolo aureo, di dimensioni  Ø e 1, si può costruire facilmente con riga e compasso secondo la tecnica indicata nell’immagine sotto. Click sull’immagine per scaricare il dwg.

A partire dal rettangolo aureo si può costruire la spirale aurea.

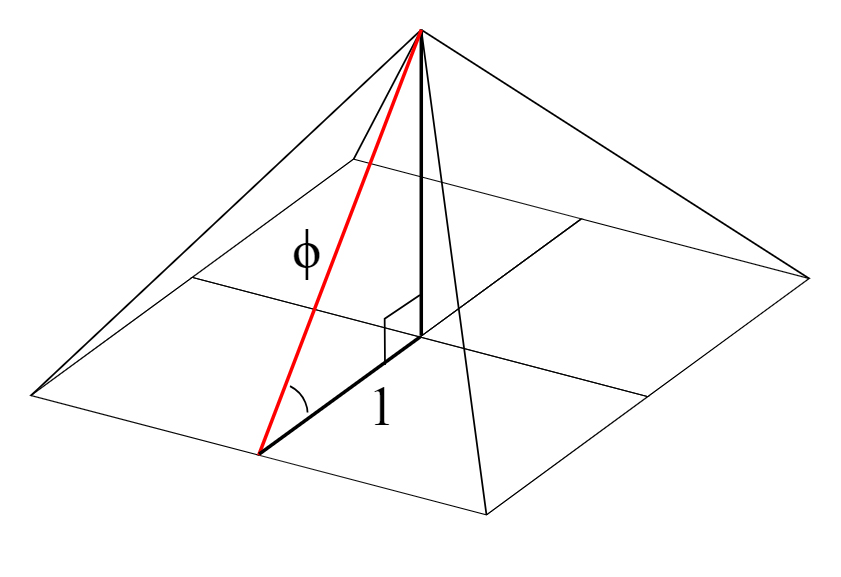
Pare che questi rapporti fossero noti fin dai tempi degli egizi, in quanto si ritrovano come particolari rapporti armonici nello studio delle dimensioni della piramide di Cheope. Analoghe proporzioni si riscontrano anche sul Partenone di Atene.

Volendo costruire una sequenza di rapporti in cui si conservi costantemente la relazione aurea tra le nuove grandezze si può procedere come segue:

(1-x):x=x:1=1:(1+x)=(1+x):(2+x)=(2+x):(3+2x)=(3+2x):(5+3x)=(5+3x):(8+5x)=
(8+5x):(13+8x)=(13+8x):(21+13x) ……

Le sequenze numeriche che abbiamo così ottenuto indicano proprio la stretta correlazione con lo nello sviluppo della successione di Fibonacci. Questa con l’aumentare dei valori si approssima sempre di più ad una progressione geometrica di ragione Ø.